Median Filters
A small overview for how median filters work.
Median filtering is a smoothing technique that can give better results than moving averages for some types of data. What is useful about median filters for our purposes here, is that they are good at removing short disruptions to a signal whilst doing a reasonable job of preserving the overall shape.
For instance, here’s a sine wave that’s been disrupted by a series of spikes (blue line), and the result of running a median filter (the dotted red line) over this. We would call these spikes outliers.
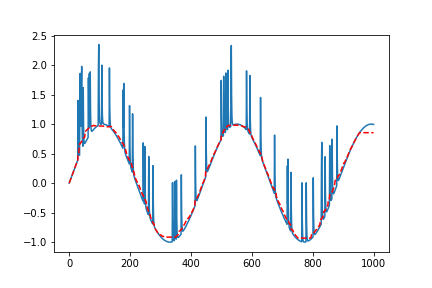
A median filter applied to a sine wave disrupted by short spikes
A median filter works in a very different way to more common audio filters (low-pass, high-pass etc.). We slide a window across our data, and replace the center value of each window with that window’s median. For example, if one of the windows has a single spike in it and the other values conform to the sinusoidal, the computed median value will likely be much closer to the stable trajectory of the signal and filter out the anomylous jumps in values.
We can see the process at work below, applied to the same case as above. The shaded area is the window, and the horizontal bar shows us where the median is at each point.
