BufSTFT

Perform an STFT on an audio buffer

Because a wealth of resources explaining the Fourier Transform in more general terms already exist, the focus of this reference is going to be on the practicalities of using it within FluCoMa. We recommend you visit the Fourier Transform page first for more detailed information on BufSTFT’s parameters windowSize, hopSize, and fftSize, as well as more general information on the Fourier Transform. If unfamiliar with the Fourier Transform or digital sampling, we highly recommend this interactive explanation.

Common Terms and Initialisms

• Fourier Transform: a mathematical operation that decomposes a continuous signal into sine wave components
• Discrete Fourier Transform (DFT): a mathematical operation that computes a Fourier Transform on a discrete signal
• Fast Fourier Transform (FFT): an algorithm for efficiently and quickly computing a DFT on a digital signal
• Short-Term Fourier Transform (STFT): segmenting a signal in to windows and performing an FFT on each window to consider spectral change over time

Re-synthesising

One reason the STFT is so commonly used is that it is possible to transform the information from the frequency domain back into the time domain. For any given FFT frame, if no magnitudes or phases are changed at all, it is possible to perfectly reconstruct the original signal of windowSize samples. We can then sum together our overlapping segments of windowSize samples (spaced out by hopSize) samples to reconstruct the original buffer (this process is called overlap-add). BufSTFT can perform this by supplying a buffer for both magnitude and phase, specifying inverse = 1, and passing a buffer to resynth for writing the re-synthesized signal into.

When we make our segments, it is common to apply an envelope to them, called a window function. Different window functions have different requirements for being able to provide perfect reconstruction, usually specifying what hopSize to use in relation to a windowSize (also called an overlap factor which is windowSize / hopSize). FluCoMa uses a Hann Window, for which, the overlap factor should be an integer greater than or equal to 2 (the windowSize should be at least twice as big as the hopSize). This is why FluCoMa’s default hopSize of -1 indicates to use a hopSize equal to windowSize / 2 (which is an overlap factor of 2).

Changing Values in the Frequency Domain

As said above, if no magnitudes or phases are changed at all, the original signal can be re-created using an inverse FFT (and an inverse STFT if there are many windows of analysis). However, if even one magnitude or phase is modified the original cannot be exactly reconstructed. This may be useful, for example, modifying some of the magnitudes before re-synthesis can adjust the loudness of a band of frequencies in the original signal (sometimes called spectral filtering). Generally speaking this is how many of the spectral processing algorithms in FluCoMa operate (AudioTransport, BufNMF, HPSS, and more).

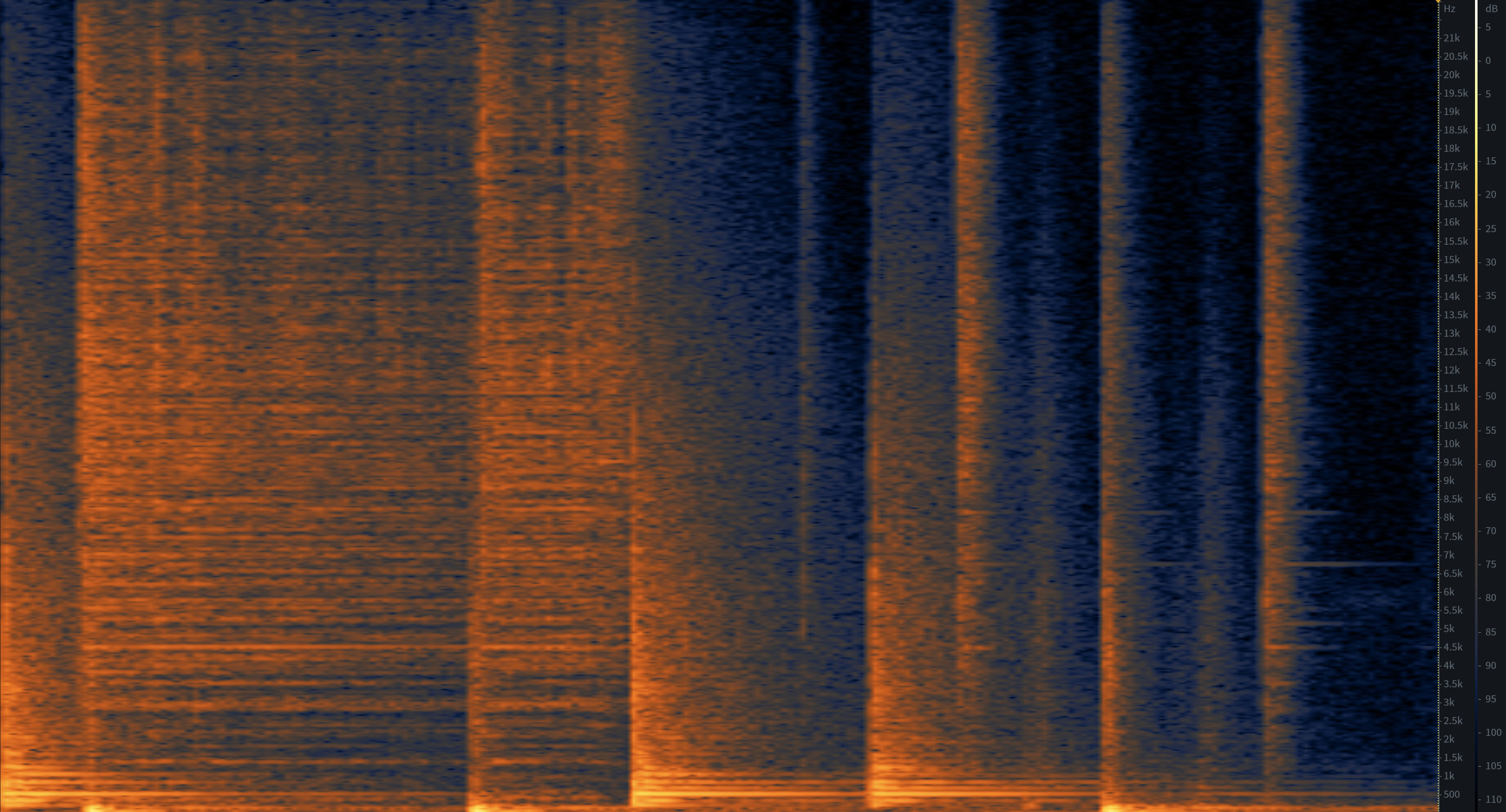
One common artefact of these adjustments is spectral smearing, which is when the time position of an event within an analysis window, becomes less clear. When all the analysis windows of an inverse STFT contain spectral smearing, it gives the signal a blurry, or chorus-y sound. If the analysis window contains a transient that is “smeared” it can be called “pre-ring”, meaning that the spectral sound of the transient can be heard prior to where it originally occurred in the analysis window. It sometimes sounds like a brief crescendo to to the transient, caused by the fade-in of the window function.

In order to avoid pre-ring or spectral smearing, one might use a smaller windowSize, so that any smearing that might happen is contained to smaller segments of time. Of course the trade off for this is less frequency resolution, which may mean less precision in the analysis or a less distinct spectral transformation by the processing algorithm.